Odometry and Navigation

(This is a saga, in that I'm appending what I'm learning as I go. So it may not make sense if you think I wrote it all at once. --jonh 5/6/96) Our robot is equipped with shaft encoders, an IR emitter-detector pair at each wheel pointed at a disc of alternating radial stripes attached to the wheel. The encoders accumulate "clicks" in a CPU register with each passing stripe.

I have been working on some SE(2) (translation plus rotation) matrix manipulation routines which attempt to track the path of the robot through 2-space based on the shaft encoder clicks, as well as the known direction that each wheel is being driven by its motor.

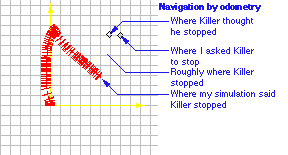
This technique has been successful in improving the usefulness of the shaft-encoder odometry, but it still needs work. In the diagram below, I asked Killer to move to the point (0,70), and then to (70,70). As you can see, the robot and the simulator (both of which share the same matrix code) don't even agree on the path taken by the robot.

I'm hoping to get the odometry to be reliable enough that it at least gives a rough estimation of position and orientation, which when coupled with sonar information, should help Killer determine his location on an internal map.

So it turned out that the problem was an incorrectly implemented FDIV (floating point divide) routine in the software floating point routines. I found an updated version of the code, and patched it into the on-board interpretter. Now the robot does a much better job of reaching its target:

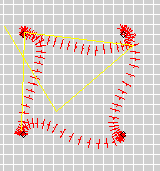
As you can see, the robot at least thought he made it to his assigned destinations. In reality, the coarse grain of the shaft encoders on the wheels (16 ticks per revolution) accumulated a lot of error throughout each turn manuever, so that the robot actually followed a path something like the yellow one shown. (Drawn from memory.)

But, it's sure an improvement! In case you're wondering, some better robots use shaft encoders with 2000 ticks per revolution. So it's understandable that there's some error.

And probably a lot of that error comes from the twisty contortions he traverses at each vertex. This is due to our correction algorithm, which wanders along, thinking everything's okay, then suddenly at the last minute, realizes how far off-course he is, and swoops in for the turn.

This behavior will be corrected in three ways:

I'm replacing the motor control code with layers, one of which statically corrects for the linear mismatch in the power of the wheel motors. This will help prevent the inital swerve in the first place.
For odometry-only path tracking, instead of aiming for the target point, we'll aim for a point on the desired path some constant distance ahead of the robot. This will help him take notice of his drifting ways well before he reaches his target.
However, we expect our main mode of locomotion to be wall-tracking (using the sonar), with the odometry used as "hints" to resolve the "events" noticed by the sonar into identifications of features from our map. Thus the odometry will only be trusted for short stretches, and it will be regularly anchored to known map locations as features are detected. And for simply travelling straight; in general, walls are pretty darn straight.