A Kohonen Network is a breed of neural network designed to group similar inputs together by having them represented by nearby neurons in a neural network. After the net is trained, each neuron represents a particular input feature vector, and domain of inputs has been organized spatially across the field of neurons in a way that reflects the original organization of the input data.
One way to visualize this process is as follows. The input is a set of feature vectors in n-space. These vectors will be mapped onto the field of neurons in m dimensions. A particular feature vector is mapped onto the neuron which most closely resembles it; in this way, we can represent all possible inputs with a finite number of neurons. We can think of the output of the net being the discrete vector ``address'' of the winning neuron.
In my program, input vectors are confined to the unit cube, and each vector is displayed as an RGB triplet color. The neural net is a flat surface (2-space), so m=2. It's certainly conceivable to construct neural surfaces of greater dimension, but two dimensions illustrates the point quite handily, and is easy to display and visualize.
A Kohonen net has the special property that it does its best to preserve continuity. That is, if two colors are nearby each other in the input space, they will be nearby each other in output space. In fact, this continuous mapping turns out to be simply the topological stretching of a figure in n-space into a corresponding figure in output space.
Of course, the network isn't perfectly successful at this task, for a number of reasons. First, some figures simply cannot be mapped continuously into 2-space. Consider, for example, the solid cube: it just can't be flattened into the plane. Secondly, the network is constructed of a collection of discrete neurons, rather than a continuous surface. Therefore, sometimes continuity appears to get lost: If one color region gets stretched into a long blob on the neuron surface, then two nearby colors may appear distant on the map. There is still a continuous transition between them, but it is lost in the discrete steps of the neurons. I.e., Kohonen nets preserve continuity, but they don't care much about preserving distance.
Finally, Kohonen nets go about constructing this mapping in a fairly haphazard way, examining only one input vector at a time. In light of this, they do amazingly well at their task. With badly tuned parameters, they construct rather poor mappings; even with good tuning, the net often builds its way into a corner, causing it to have to break continuity for some regions.

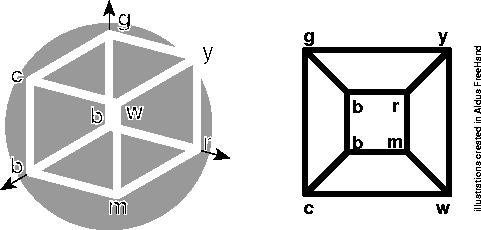
Figure 1. Left: The edges of the unit cube, as colored in RGB space. Right: A correct mapping into 2-space which preserves continuity.
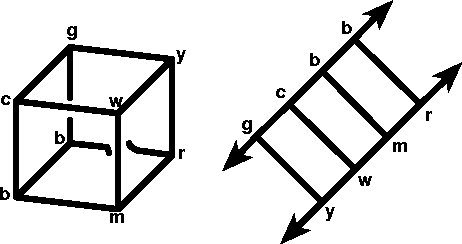
Figure 2. Left: A frustrated Kohonen net can't quite continuously connect two of the original edges. Right: A correct solution discovered by the network relies on the ``wrap-around'' shape of toroidal 2-space. The arrows indicate where the figure connects with itself.
Overall, however, self-ordering maps are surprisingly successful. Even humans have to think a little bit to discover how the edges of a cube can be mapped into 2-space. When the Kohonen net solved this problem, it almost always preserved the continuity of at least ten edges, and once even came up with an unexpected but correct solution which takes advantage of toroidal 2-space (See Figures 1 and 2).
Invoking som with no options causes it to read options from som.defaults and run in default mode. Invoking som with an illegal option displays a usage message like the one below.
-I <filename> specify input (vector) filename.
-O <filename> specify output (map) filename.
(<filename> may be "stdout".)
-a specify append to output mode.
-A specify overwrite output mode.
-m{hcdbrzet} specify map parameters.
-m{RC} <int> specify map row or column dimension.
-n{wWhsr} specify neighborhood options.
-nR <int> specify neighborhood radius.
-l{AGD} <value> specify learning parameters.
-v{gGep} viewing mode, each vector or per V vectors.
-vV <value> specify update rate in vectors.
-x display map in an X window.
-X don't display map, just write output file.
Any option that can be used on the command line may also be used in som.defaults, and options are written at the top of map output files for future reference.
Input files are simply a series of lines, each with three ASCII floating point values. Each line represents one input vector. Many pre-generated input figures are available in the directory col/. Output files are written in two parts. The first series of lines are lists of options (to be interpreted by mapview when displaying previously generated maps); the rest are rows of ordered triplets (again in ASCII) representing neuron values in the map. Output files may contain comment lines preceded by a `#' symbol. The append option allows you to keep tacking new maps onto a single output file, for sequential viewing with mapview.
The X options allow you to either run som in background mode or with a graphical interface. The remainder of the options have analogous input fields in the graphical control panel, and it is easier to see their influence there.
The current som.defaults file specifies a graphical interface. Run som to explore the options as you read this. If you don't run som at least once, I'm going to be very disappointed. Be sure to run it from a color workstation. The Mac won't allocate enough colors, either.
The program will begin by loading a default set of input colors, and displaying input space in a 3D window. Then it will randomly initialize the neurons and begin the training process.
A Kohonen net trains in the following cycle:
In som, you have a wide variety of options with regard to just how these steps are performed. First, you may configure the arrangement of the neurons. You may input the desired dimensions of the map, measured in neurons. A hexagonal arrangement makes each neuron have six equally near neighbors; a square (Cartesian) arrangement gives each neuron four closest neighbors. Hexagonal maps must have an even number of rows. You may leave the map a simple box figure with an outside boundary, or close the figure into the surface of a torus or donut. The map can be initialized to either zero (black) neurons or neurons representing a uniform random distribution of inputs. The euclidean versus taxicab option affects the measure of distance used for feature space in step 2.
The neighborhood properties affect step 4. You may input the initial radius of the neighborhood. On Cartesian maps, the shape of the neighborhoods may be either square or circular. Neighborhood shape is confined to a hexagon for hexagonal maps. The ``Weighted'' option, if checked, causes neighbor neurons modified in step 4 to be affected less as a function of their distance from the center of the neighborhood. The winning neuron is modified according to the full value of alpha as in step 3, and more distant neurons are modified according to alpha*f(distance), where f is a normal bell curve. Without weighted neighborhoods, every neuron in the neighborhood is affected in the same amount as the winning neuron.
The learning parameters include alpha, alpha goal, and decay rate. As it happens, training is most effective when alpha and the neighborhood radius are allowed to decrease with time. To accommodate this, the program has a decay feature. Every decay times through the training loop, the neighborhood radius is decreased by one, and alpha is moved closer to alpha goal. The value of alpha is determined by linearly interpolating between its initial value and the goal, so that alpha arrives at alpha goal just as the neighborhood radius arrives at one. The training is stopped after training with a radius of one, since not many neurons would be affected in a neighborhood of zero radius.
The map view is updated every vectors times through the training loop when the per vectors option is chosen. Updating the view with each vector makes it convenient to see the effects of varying the neighborhood options, at the expense of speed. Updating with each vector is different from updating per 1 vectors in that the each vector option only redraws those neurons that appeared in the neighborhood (to save a little time). Try watching the very beginning of a training sequence in each mode--you'll see directly how the weighting and shape of neighborhoods affects neurons.
The grid checkbox draws the inverse image of the mapping as a grid surface in input space. The window which displays input vectors will have a grid surface superimposed on it. Each node on the grid corresponds to the value of a particular neuron. This lets you directly visualize how the map is stretching to fill feature space. I recommend leaving the grid display off, then turning it on to display a particular grid of your choice; otherwise, the program spends a lot of time redrawing.
All of the control parameters only affect the initial settings of the map; they will not change a map in the calculation process. To invoke the changes, discarding the current map, click Reset. Stop will pause the training so the display can be inspected; Continue will resume calculation without reloading the parameters and initializing the neurons. Read re-reads the input file; it is functionally identical to Reset, but it lends a nice symmetry to the display. Write stores the map to the output file as previously described. (When running in background mode, the map is automatically written after training ceases, and the program terminates.) Quit is fairly self-explanatory. I included a sentence on it for prosaic closure, and because the capital Q's in this typeface are very pretty.
have more separate paths leading into them. However, for most problems, the Cartesian map, even with square neighborhoods, performed about as well. Initializing the neurons to random values improved performance by helping key points of the final image form at some distance from each other and build continuous paths between each other. Zeroing the neurons made a blob which grew out from an initial point, and this often made it difficult for the network to create separate, smooth paths.
Euclidean versus taxicab distance had very little effect on the network, but it wasn't extensively tested. Consider that if we are asking the network to associate similar vectors, then its association is certainly going to be a function of our definition of distance. Changing the distance measure, then, doesn't change the network's behavior in an unexpected way.
The network did its best when it started with neighborhoods about an eighth of the area of the map. If the neighborhoods are too large, then the input vectors just spend the first several decay periods blasting away at each other, wasting lots of CPU cycles. Starting with neighborhoods that are too small causes the network to terminate training before it has connected all of the regions of features together. As I've mentioned, neighborhood shape was of very little consequence; even less compared to the effort spent coding the different options.
Weighted neighborhoods have a tremendous influence on the ability of the network to generate continuous transitions. Apparently, when the neighborhoods are large, weighting creates a smooth transition between the centers of two feature neighborhoods, setting that path up to be refined into a continuous transition. As the radius decreases to one or two, the weighting has very little effect, and the training has the effect of sharpening boundaries where there should be not a continuous transition but a discrete division.
The decay rate should be of about the same order as the number of feature vectors, so that with each neighborhood size, the network is exposed to a fair sampling of input space. Alpha should start out fairly high, between 0.8 and 1.0, to cause the first passes of large neighborhoods to generate strong key regions to which it will later add detail with a more gentle alpha. The alpha goal should be greater than zero, so that the smallest radii have the boundary-sharpening effect described above. It should be weaker than alpha, though, so that later passes don't try to disturb the order initially set up when alpha was large. A value around 0.2 works nicely.
The full feature figure is simply vectors distributed uniformly all over the unit cube. Note in the trained map that you can locate points corresponding to all eight corners of the cube. Furthermore, every color squishes smoothly into every other color. As we'd hope, the entire map is smooth (continuous), since every feature vector was nearby some other vectors in every direction.
Now clearly, a Kohonen net can't squish a solid cube into 2-space any better than a mathematician can, and a mathematician can't. So what compromise has the network come up with? At this point it is best to introduce another way of thinking about the self-ordering process. Recall Jeremy's demonstration of Neural Graphics, in which a blob stretched out into a grid in feature space, trying to fill up the area of the feature figure (for example, a triangle). That's the image which best depicts this situation. Use the view grid feature to see a graphic display of the inverse mapping from all of output space (every neuron in the map) back into a surface in input space.
Connect the neurons with a grid, each neuron to its closest neighbors. When the training began, the grid in feature space was either condensed into a point at the origin (for zeroed neurons) or randomly contorted throughout the unit cube. As it trained, the key regions, such as a spot of bright red, represents a portion of the grid that has been pulled into a corner of the cube. Because of how Kohonen maps preserve continuity, nearby points on the grid have been pulled near that corner as well, helping form the grid into a surface rather than a chaotic blob. Clearly, since the surface is two dimensional, the final grid is simply a wavy surface wandering through the cube, trying to distribute itself uniformly throughout.
One final interesting observation about the figure full is how it seems to produce almost independent stripes of red, green, and blue. Furthermore, notice that they're as orthogonal to each other as they can be in 2-space. (I.e., there are only two orthogonal vectors in 2-space, so two colors are forced to share one and line up parallel to each other.) The secondary colors (magenta, cyan, and yellow) show up at the intersections of the primary stripes just as they would if the stripes were produced by independent light sources, and the secondaries were locations of additive color. The network showed this behavior repeatedly with the full cube as input. I conclude from this that the network is responding to the fact that the input space has three very clearly defined basis vectors, and those bases stood out clearly in the self-organization of the map. Imagine that: a neural net that does linear algebra!
Another interesting figure is bluered, so named because it contains two planar regions, one with colors which have no red in them, and others which are saturated with red. The two regions are separated by the volume of the unit cube. Notice how the map is sharply divided into the appropriate blue-green and red-white regions. Also, observe how each planar surface was mapped in a straightforward manner. In the red region, you can find the key regions for red, yellow, magenta, and white, and the area bounded by those points is a simple morph of the red plane from input space. Examine the corresponding inverse image grid, and you'll see how the surface has two parts, each squished flat onto one of the plane figures. Since there is only one large surface, notice the stringy web crossing over the chasm in between, with almost no neurons living in the gap. Remember this when we come to the concluding discussion.
In the introduction I discussed mapping the edges of the cube; data for that figure can be found in edges. The file star contains a figure with the four diagonals of the cube, forming an eight-pointed star. Notice how grey, the key point which must join with each of the tentacles of the figure, ends up getting stretched so thin that it looks almost disjoint on the map. This is a manifestation of the discrete continuity problem discussed earlier. Of course, on some tries, the map may actually fail to keep the grey area connected, which is a simple error.
The file circle is simply a circular collection of vectors. The map turns out to be a contortion of the closed circle, and it fills up output space. Try mapview -tile out/circle to see the map tiled with itself, which is an appropriate way to look at a toroidal surface. It generates a repeating pattern which tiles 2-space. Escher would be proud.
A circle with a bar poking through it is stored in hoop. On some trials, the Kohonen net has been successful in removing the bar from the circle and organizing it separate from the hoop. A logical extension of this is the data in link. In theory, the Kohonen net should be able to separate the two circles and treat them independently of one another. (I have yet to make this successful; however, I think that this problem is very sensitive to having the training parameters just right, but not unsolvable.) This sheds a little more light on what sort of mappings are actually being created by the neural network: It is not always generating a continuous mapping from the volume of the unit cube into the area of a square. If it were, the links could not be separated--they are topologically tied to each other. In fact, it's only creating that mapping in the case of a feature vector set like full. Instead, it's creating a mapping whose domain is exactly the points of the figure in input space, and whose range is exactly the area of the square.
However, their power lies in their ability to perform fantastic feats of linear algebra and topology. They can compress figures from some high dimensional space into a smaller one (such as 2-space) while preserving a crucial feature of the figure, such as continuity. This is rather useful, as it can extract information about a multidimensional feature space too difficult to visualize for humans, and display it in a small, easily handled space, in fact filling that space with exactly the critical information it has preserved.
Better yet, recall the surface generated for the pair of planes in bluered. What if we limited the elasticity of the surface? If it became too stretched between two neurons, we tear the connection between those two neighbors. In the example, the each plane would end up with a surface of its own, and the two surfaces would be unconnected. Now the network is extracting even more features about continuity on its own merely by giving its surface a finite tear strength.
I wonder if Kohonen knew just what kind of feature extraction his networks were doing?